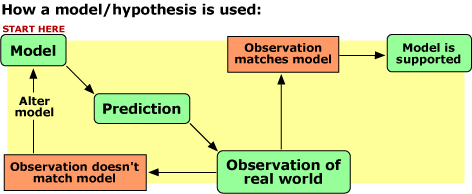
Doctors and researchers thought that cycling could indeed help reduce levels of antibiotic resistance, and clinicians began testing the idea in hospitals in 2000. At around the same time, Carl and his colleagues began investigating the question using computer models. A model, in this case, is a set of rules about how the components of a system interact (e.g., how rapidly a single patient will evolve a resistant infection, how likely that infection is to be passed to another patient, etc.) that may be represented by a computer program or a set of equations. A model is a hypothesis about how a system works and what factors affect it. The hypothesis/model generates predictions (e.g., if this set of rules is true, then we’d expect to observe X when we change antibiotics every six months). Those predictions can then be compared to what is observed in the real world — the more often they match, the more likely it is that the model represents what is important in the real world. If predictions and observations do not match, then some aspect of the model probably needs to be changed.

Carl and his colleagues built a computer model of patients in a hospital being treated with antibiotics, which made a surprising prediction: cycling would not work. In their model, cycling through antibiotics did not reduce overall levels of antibiotic resistant infections. Is this prediction accurate? Well, the results from the clinical trials are starting to come out, and as Carl puts it, “They largely agree with our predictions…Basically, cycling doesn’t seem to be working. So this was a case where we predicted that cycling won’t be a useful tool. If we were right, that would mean bad news for our efforts to control antibiotic resistance — so we actually hoped we were wrong. But I’m afraid it’s looking like we were right.”

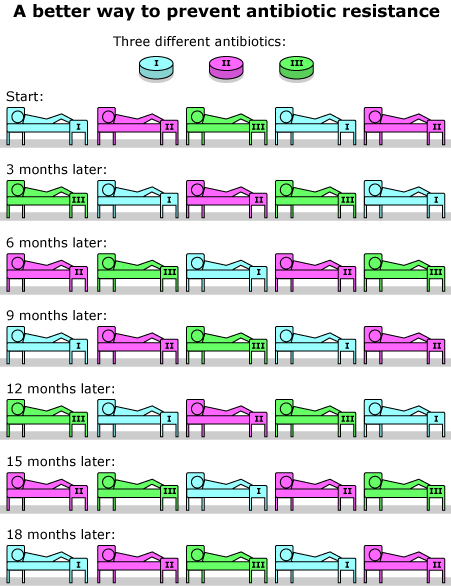
If the researchers had merely tested the cycling strategy in a hospital, that would have been the end of it — we would only have learned that cycling, as set up in the experiment, doesn’t work. But Carl’s model helps us understand more about what went wrong with cycling and how to fix it. The model suggests that having all the patients in the hospital taking the same antibiotic at the same time actually makes it easier for the bacteria to adapt to the drug. Similarly, the model suggests that a better way to slow the spread of antibiotic resistant bacteria is to treat different patients with different antibiotics (as shown below), making it more difficult for a bacterium with resistance to a particular antibiotic to succeed when it infects another patient. Of course, this too is a hypothesis, and the strategy is subject to testing in the real world. Nonetheless, Carl’s model supplies valuable information to consider when designing the next experiment.

Even without Petri dishes and test tubes, modeling is an essential tool for learning about the natural world. Biological systems are complex, and as Carl explains it, “The reason we like to use mathematical models is because when we try to understand the processes underlying the spread of antibiotic resistance, we want to be formally rigorous, we want to make sure that each step of our thinking is a natural, correct, and logical consequence of the previous one. And at its core, mathematics is just a beautiful formalism for rigorous, logical thinking.”