Emilia used mathematical modeling techniques to demonstrate that EPAS1 stood out from the crowd of other genes. What can a set of equations and a computer program tell you about biological processes? A lot, it turns out.

The idea of mathematical modeling in population genetics is this: Biologists have a pretty good understanding of how evolutionary processes like genetic drift and natural selection change allele frequencies from one generation to the next. This basic model of evolution is written up in the form of a computer program with different parameters (such as population size and migration rate) that can be varied to match the details of a situation of interest (e.g., the evolution of the Tibetan and Han populations over the last 100,000 years). Some of these parameters might be fairly well known (e.g., when human populations began to leave Africa), and other parameters may be poorly known (e.g., when the Tibetan and Han populations split). When the model is run over many generations, it simulates evolution. In this sense, the computer acts like a laboratory in which we can see how virtual populations evolve under different conditions (i.e., different parameters). Each set of parameter values represents a slightly different model of the evolutionary history of the population. To figure out which model is the best hypothesis about the true evolutionary history of the population, scientists compare the outcomes of the model to their observations of the actual population. For example, they might compare the level of heterozygosity in different virtual populations to the true level of heterozygosity in the actual population. A close match between model outcomes and real observations means that the data support that particular model.

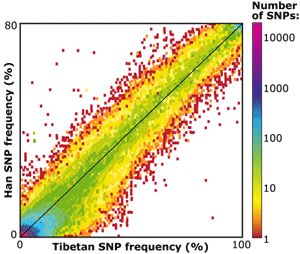Emilia built a model that simulated the Tibetan and Han population histories from the time the group was still living in Africa, through their migration to Asia, their split when a large group moved to the Tibetan Plateau, and the subsequent migration between the groups. She varied different parameters (such as the population size at different points in time, the timing of the split, and the level of migration) and found a model that closely matched the level of variation observed in the Han and Tibetan populations (i.e., the level of variation seen in the graph of allele frequencies shown here). Of the models analyzed, the best-fitting model suggested that the Han and Tibetan lineages split less than 3000 years ago.

Using this model, she simulated what level of allele frequency differentiation was likely to be observed if the variants in EPAS1 were not under selection (i.e., were changing due to genetic drift and migration alone) and compared these results to the actual level of differentiation observed. Her simulations showed that it was extremely unlikely that such a high degree of differentiation could come about without the action of natural selection. The team had found their gene!